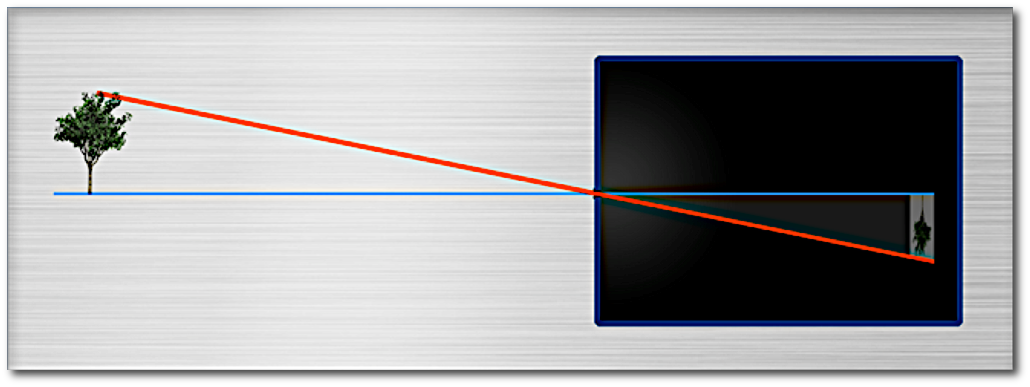
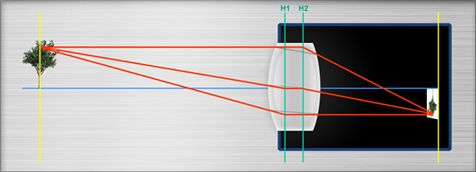
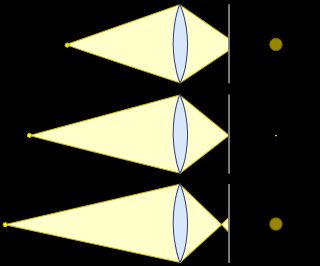
Um auf kürzere Entfernungen zu fokussieren müssen s-mount Objektive „herausgeschraubt“ werden. Das scheint sich auf den ersten Blick stark von größeren Objektiven wie C- oder CS-mount Objektiven zu unterscheiden, die über einen Fokusring zu manuellen Fokussierung verfügen. Wenn der Fokusring jedoch gedreht wird, wird dabei auch in größeren Objektiven (mindestens) ein Paket von Linsen weiter vom Sensor entfernt. (Es gibt ein paar Ausnahmen von Objektiven bei denen mehr als ein Linsen-Paket synchron bewegt werden. Eines davon vielleicht auch Richtung Sensor.)
Geschätzt mehr als 95% aller Objektive verhalten sich aber wie folgt:
Sei das Objektiv zunächst auf ![]() fokussiert.
fokussiert.
Was passiert, wenn die Entfernung zwischen dem Linsenpaket und dem Sensor erhöht wird, zum Beispiel durch herausschrauben oder durch drehen des Fokusrings?
- Der maximale objektseitige Öffnungswinkel bleibt gleich … weil sich die Optik nicht ändert
- Der maximale bildseitige Öffnungswinkel bleibt gleich … weil sich die Optik nicht ändert
- Die maximale Menge unterstützer Bildpunkte bleit gleich … weil sich die Optik nicht ändert
- Die Blendenzahl F# ändert sich zur “Working F#” (auch effektive Bendnzahl genannt) :
Die Blendenzahl F# eines Objektivs ist nur für unendlichen Objektabstand definiert. Wenn ein Objektiv auf unendlich fokussiert wird, befindet sich der das Bild in der Brennebene, also auf dem Sensor, weil wir auf unendlich scharf gestellt haben. Die Blendenzahl F# ist dann definiert als: Brennweite dividiert durch den Eintrittspupillendurchmesser (= den scheinbaren Durchmessers des „Lochs“ in der Linse, wenn wir von Objektseite schauen= “EPD”)Die working F# („wF#“) ist etwas anders definiert:
![Rendered by QuickLaTeX.com \[wF\# = \frac{Brennweite + herausgeschraubter Weg}{EPD}\]](https://www.optowiki.info/de/wp-content/ql-cache/quicklatex.com-7ded7e4afbb03d4b151afcea944c4f03_l3.png)
![Rendered by QuickLaTeX.com \[ = F\# + \frac{herausgeschraubter Weg}{EPD}\]](https://www.optowiki.info/de/wp-content/ql-cache/quicklatex.com-5b8749e9f3296ceab4f36b296dd6a21b_l3.png)
Für eine 1:1 Vergrößerung (Objektgrösse = Sensorgröße), muss man ein Objektiv um die Brennweite herausschrauben, also 12mm für ein f=12mm Objektiv : 4mm für ein f=4mm Objektiv, 50mm für ein f=50mm Objektiv). Da die Gewinde oft nicht lang genug sind, kommen Zwischenringe zum Einsatz
Für den 1:1 erhalten wir also
![]()
(weil das Objektiv um f herausgeschraubt wurde, erhalten wir
![]()
)
Das gleiche Ergebnis erhalten wir aus obiger Formel für M=1:
![]()
Für ein Objekt im unendlichen ist kein herausschrauben nötig, also gilt wF# = F#.
Die Vergrößerung eines Objektivs im unendlichen ist Null, weil der Sensor klein ist und das Objektiv auf der objektseite unendlich viel sieht. (Bei sternenklarer Nacht z.B. Hunderte Galaxien). Wir erhalten also aus obiger Formel :
![]()
- Die Helligkeit des Bildes ändert sich:
Die Lichtmenge die den Sensor erreicht wird durch wF#, die working F# (= effektive Blendenzahl). wF# hängt vom Durchmesser der Eintrittspupille ab , aber die Helligkeit hängt von der Fläche der Eintrittspupille ab.
Die effektive Blendenzahl wF# eines 1:1 Objektivs ist
![]()
, also das Doppelte der wF\# in der Unendlich-Position
Die Helligkeit sinkt also um den Faktor 2^2 = 4 im Vergleich zur Helligkeit im Unendlichen
- Im Allgemeinen sinkt die Auflösung: Der kleinste mögliche Punktdurchmesser den ein (beugungsbegrenztes) (lies „perfektes“) Objektiv erzeugen kann ist durch den Rayleigh Durchmesser gegeben:
![Rendered by QuickLaTeX.com \[ D = 2 \cdot 1.22 \cdot wF\# \cdot Wellenlaenge \]](https://www.optowiki.info/de/wp-content/ql-cache/quicklatex.com-2d672869d8e13c31bc3679fabd6b833a_l3.png)
Die Grenzauflösung ist die Hälfte dieses Durchmesser R = D/2.
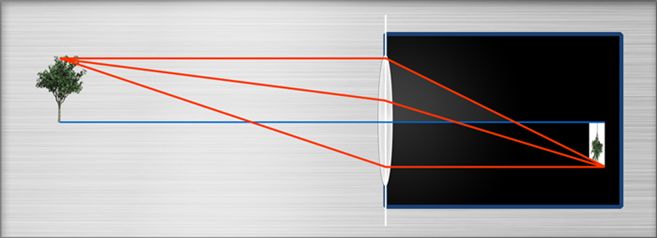
- Das Sichtfeld (Field of view, „FOV“ ) wird kleiner: Weil das Objektiv nicht telezentrische ist (sondern „entozentrisch“), erreicht das Licht das Objektiv in Winkeln > 0 am Rand des Sensors. Wir können uns den Winkel als halben bildseitigen Öffnungswinkel vorstellen.Dieser Winkel heisst (maximaler) Chief Ray Angle, CRA)
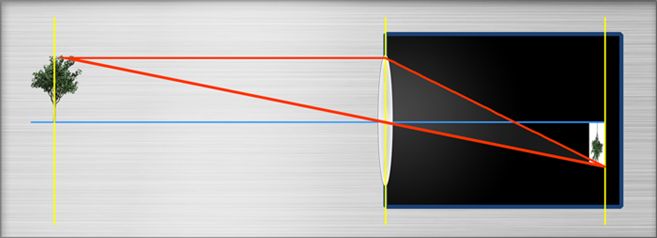
wenn das Objektiv in seiner Position ist. Erhöhen wir die Entfernung zum Sensor, so bleibt zwar der maximale Winkel gleich, aber der äußere Teil des Lichts wird den Sensor nicht mehr erreichen. Das bedeutet, dass nur noch ein kleinerer „Blickwinkel“ Richtung Sensorseite benutzt werden kann. Das bewirkt aber, dass auch auf Objektseite nur noch ein kleinerer Winkel genutzt werden kann!
Position ist. Erhöhen wir die Entfernung zum Sensor, so bleibt zwar der maximale Winkel gleich, aber der äußere Teil des Lichts wird den Sensor nicht mehr erreichen. Das bedeutet, dass nur noch ein kleinerer „Blickwinkel“ Richtung Sensorseite benutzt werden kann. Das bewirkt aber, dass auch auf Objektseite nur noch ein kleinerer Winkel genutzt werden kann! - Die Vergrößerung ändert sich. This is because the sensor keeps its size and the visible Object size gets smaller, see above
- Die Verzeichnung verbessert sich im Allgemeinen: Die Verzeichnung von Objektiven ist im Allgemeinen in den Bildecken grösser als in der Bildmitte. Weil wir jetzt aber objekt- und bildseitig kleinere Winkel verwenden, verwenden wir auch die alten Bildecken nichtmehr. Daher verwenden wir auch die Ränder der Linsen nicht mehr, wo die Verzeichnung am größten war.
- Der Arbeitsabstand ändert sich. Da die Vergrößerung durch „Sensorgrösse durch Objektausschnittgrösse“ gegeben ist (und auch durch „Bildabstand durch Objektabstand“) muss sich bei geändertem Bildabstand auch der Objektabstand ändern. Er wird kleiner.
Auch die Bildhelligkeit geht nicht um den Faktor 4 zurück, wie das bei entozentrischen Objektivn der Fall wäre, sondern das Bild bleibt gleichhell.