If the object distance changes by 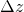 , then the image distance changes by
, then the image distance changes by
![]()
which is also the number of distance rings needed to refocus.
According to the Newtonian Image equation :
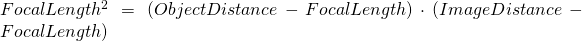
or shorter
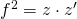
or shorter
A change of the object distance by ![]() results in a change of the image distance by
results in a change of the image distance by ![]() .
.
As refocusing does not change the focal length, also the square of the focal Length is constant:
![]()
and
![]()
which is equivalent (for z != –![]() ) to
) to ![]()
A lens with a f=50mm focal length can usually be focused from 1m. How many distance rings are required to focus it to 50cm?
The Newtonian Image Equation results in:
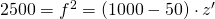
or
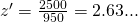
Say

and therefore
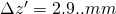
The Newtonian Image Equation results in:
or
Say
and therefore
A lens of f=50mm focal length usually is focusable from 1m. How many distance Rings are required to focus it to 20cm?
The Newtonian Image Equation results in:
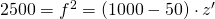
or
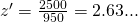
Say,
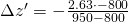
and therefore
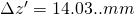
The Newtonian Image Equation results in:
or
Say,
and therefore
A lens of f=50mm focal length usually is focusable from 1m. How many distance Rings are required to focus it to 10cm?
The Newton Image Equation results in:
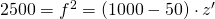
or
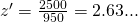
Say,
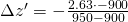
and thus
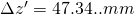
The Newton Image Equation results in:
or
Say,
and thus
Compared to the 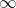 setting (= BFL) the image distance changes by
setting (= BFL) the image distance changes by
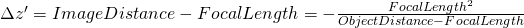
which is equivalent to the length of distance rings required to focus on the object distance.
which is equivalent to the length of distance rings required to focus on the object distance.
This is simply, because according to Newton :
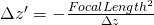
with

with
Use the following calculator for lenses focused to infinity – for example for M12 board lenses. For “finite conjugated” factory automation lenses use the second calculator.
Use the following calculator if your lens is finite conjugated , such as for factory automation c-mount lenses.
If your lens is infinity conjugated, you might want to use the calculator above.
If your lens is infinity conjugated, you might want to use the calculator above.
How many distance rings are necessary to focus an f=50mm lens to 50cm?
According to the equation above we get:
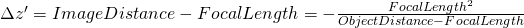
Say,
 = -5.55mm
= -5.55mm
The Back Focal Length (=BFL) increased in the 500mm position by 5.55mm compared to the setting.
setting.
According to the equation above we get:
Say,
The Back Focal Length (=BFL) increased in the 500mm position by 5.55mm compared to the
How many distance rings are necessary to focus a f=50mm lens to 20cm?
According to the equation above we get:
![]()
Say,
![]() = -16.67mm
= -16.67mm
The Back Focal Length (=BFL) increased in the 200mm position by 16.67mm compared to the ![]() setting.
setting.
How many distance rings are necessary to focus a f=50mm lens to 10cm?
According to the equation above we get:
![]()
Say,
![]() = -50mm
= -50mm
The Back Focal Length (=BFL) increased in the 100mm position by 50.00mm compared to the ![]() setting.
setting.