Ändert sich die Objektweite um 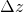 , So ändert sich der Bildweite um
, So ändert sich der Bildweite um
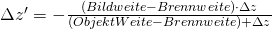
was der Länge der nötigen Zwischenringe entspricht um neu fokussieren zu können.
Nach der Newtonschen Abbildungsgleichung gilt:

oder kurz:
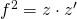
oder kurz:
Eine Veränderung der Gegenstandsweite um ![]() macht sich also in einer Veränderung der Bildweite um
macht sich also in einer Veränderung der Bildweite um ![]() bemerkbar.
bemerkbar.
Da die Refokussierung die Brennweite nicht ändert, ist auch das Quadrat der Brennweite konstant und es muss gelten :
![]()
und
![]()
was für (z != –![]() ) äquivalent ist mit
) äquivalent ist mit
![]()
Ein Objektiv von f=50mm Brennweite lässt sich i.a. erst ab 1 Meter fokussieren, Wieviele Zwischenringe werden benötigt, um es auf 50cm fokussieren?
Die Newtonsche Abbildungsgleichung liefert uns:
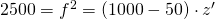
oder
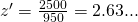
also
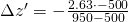
und damit
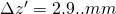
Die Newtonsche Abbildungsgleichung liefert uns:
oder
also
und damit
Ein Objektiv von f=50mm Brennweite lässt sich i.a. erst ab 1 Meter fokussieren, Wieviele Zwischenringe werden benötigt, um es auf 20cm fokussieren?
Die Newtonsche Abbildungsgleichung liefert uns:
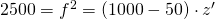
oder
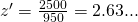
also
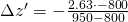
und damit
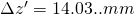
Die Newtonsche Abbildungsgleichung liefert uns:
oder
also
und damit
Ein Objektiv von f=50mm Brennweite lässt sich i.a. erst ab 1 Meter fokussieren, Wieviele Zwischenringe werden benötigt, um es auf 10cm fokussieren?
Die Newtonsche Abbildungsgleichung liefert uns:
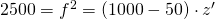
oder
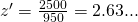
also
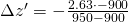
und damit
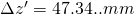
Die Newtonsche Abbildungsgleichung liefert uns:
oder
also
und damit
Im Vergleich zur 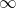 Einstellung (= BFL) ändert sich die Bildweite um
Einstellung (= BFL) ändert sich die Bildweite um

was der Länge der nötigen Zwischenringe entspricht um auf Objektweite fokussieren zu können.
Einfach, weil nach Newton gilt :
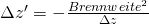
mit
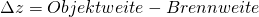
mit
Wieviele Zwischenringe sind nötig, um ein f=50mm Objektiv auf 50cm zu fokussieren?
Aus der Gleichung oben ergibt sich:

else
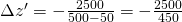 = -5.55mm
= -5.55mm
Die hintere Schnittweite (=BFL) ist also in der 500mm Einstellung um 5.55mm länger also in der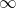 Einstellung
Einstellung
Aus der Gleichung oben ergibt sich:
else
Die hintere Schnittweite (=BFL) ist also in der 500mm Einstellung um 5.55mm länger also in der
Wieviele Zwischenringe sind nötig, um ein f=50mm Objektiv auf 20cm zu fokussieren?
Aus der Gleichung oben ergibt sich:

else
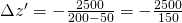 = -16.67mm
= -16.67mm
Die hintere Schnittweite (=BFL) ist also in der 200mm Einstellung um 16.67mm länger also in der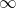 Einstellung
Einstellung
Aus der Gleichung oben ergibt sich:
else
Die hintere Schnittweite (=BFL) ist also in der 200mm Einstellung um 16.67mm länger also in der
Wieviele Zwischenringe sind nötig, um ein f=50mm Objektiv auf 10cm zu fokussieren?
Aus der Gleichung oben ergibt sich:

else
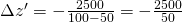 = -50mm
= -50mm
Die hintere Schnittweite (=BFL) ist also in der 100mm Einstellung um 50mm länger also in der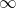 Einstellung
Einstellung
Aus der Gleichung oben ergibt sich:
else
Die hintere Schnittweite (=BFL) ist also in der 100mm Einstellung um 50mm länger also in der