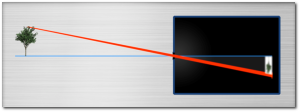
Vor ein paar Jahrunderten bemerkten irgendwelche Leute, sicher mit einigem Erstaunen, dass in dunklen Räumen manchmal ein (auf dem Kopf stehendes) Bild der Umgebung auf die einer kleinen Öffnung gegenüberliegende Wand projeziert wird.
Das alten lateinische Wort für Kammer (chamber) ist Camera.
Daher waren die ersten „Kameras“ begehbar und erhielten den Namen „camera obscura“ ( = „dunkle Kammer“). Eine der ersten Anwendungen war die Portrait-Malerei und die perspektivisch richtige Malerei.
Das gleiche Prinzip wir in sogenannent „pinhole-Kameras“ oder „Lochkameras“ benutzt:
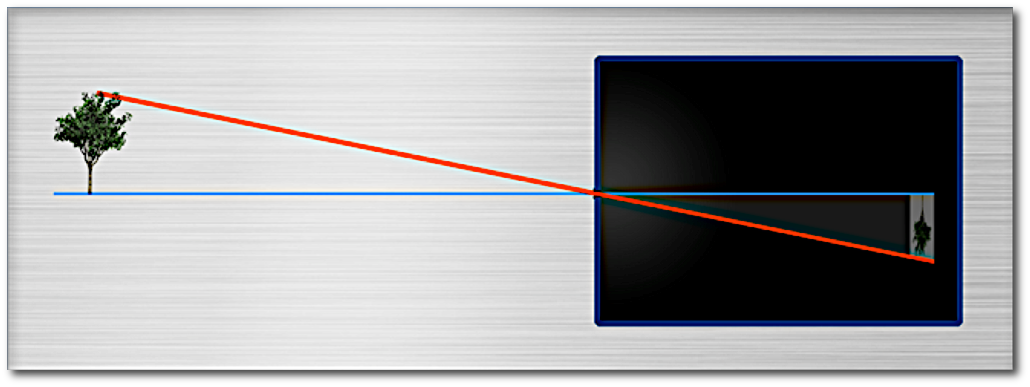
Es wird sofort klar, warum das Bild auf dem Kopf steht.
Der Vorteil ist, das das Bild dort erscheint, wo man es mathematisch erwarten würde. Es gibt keine Verzeichnung! (Rechtecke auf Objektseite werden auf Rechtecke auf der Bildseite abgebildet). Es gibt keine (sichtbare) Abhängigkeit von der Wellenlänge. Die Schärfentiefe scheint unendlich.
Der Nachteil is ist, dass das resultierende Bild sehr dunkel ist, (der Raum muss also noch dunkler sein, damit das Bild überhaupt gesehen werden kann. Die Benötigte Belichtungszeit um ein Bild mit heutigen Kameras aufzunehmen kann leicht mehrere Minuten betragen!
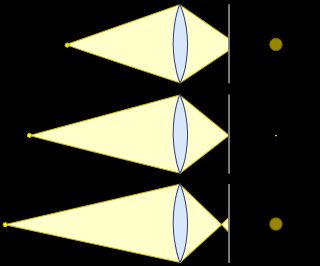
Idee: Man könnte ein größeres Loch verwenden:
Dummerweise wird das Bild jetzt aber nicht nur (wie beabsichtigt) heller, sondern auch verschwommener, da das Licht nicht nur durch die Lochmitte kommt und den Wunschbuildpunkt beleuchtet. Nein, seine Nachbarn werden auch gleich mit belichtet. Das Licht was eigentlich nur für die Nachbarn des Bildpunktes bestimmt war, landet stattdessen auch auf dem Bildpunkt.
Als Ergebnis ist das Bild eines Objektpunkts nicht nur ein Punkt im mathematischen Sinne, sondern stattdessen eine kleine Kreisscheibe, der Sogenannte „Unschärfekreis“ oder „Circle of Confusion“ (CoC).
Für nahe Objekte sogar noch grösser. Die „Auflösung“ ist also sehr schlecht.
Wunsch: Jeder Bildpunkt sollt ein im mathematischen Sinne ein Punkt und keine Kreisscheibe sein.
Idee: Man kann eine biconvexe Linse („Sammellinse“) in die Öffnung einsetzen 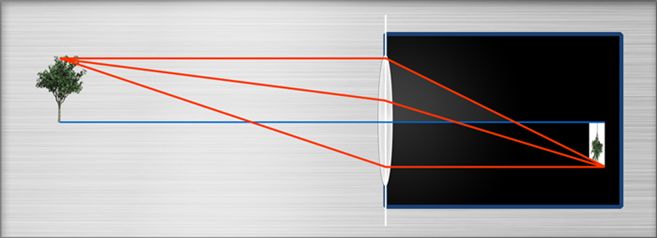
Wie kann man Position und Größe des Bildes von Objekt und Objektpunkten voraussagen?
Zwei einfache Regeln finden Anwendung:
Strahlen durch die Mitt der Linse gehen gerade durch die Linse.
Strahlen, die vom Objektpunkt paralllel zur Optischen Achse verlaufen werden durch den Brennpunkt der Linse abgelenkt („gebrochen“).
Dort wo diese beiden Strahlen sich treffen ist dasBild des Objektpunkts.
Wir notieren:
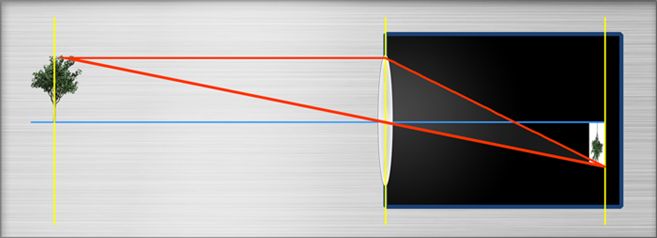
Sind Bild und Objektentfernugnen gegeben können wir die Brennweite der Linse bestimmen.
Dieser Ansatz wird in fast allen online Brennweitenrechnern verwendet.
Im „richtigen Leben“ bemerken wir jedoch eine Abweichung zwischen den theoretischen Werten und den tatsächlichen Entfernungen:
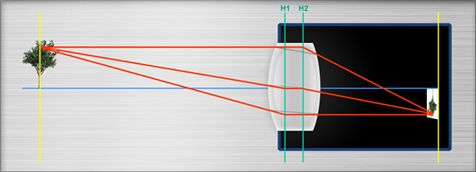
Durch diesen Unterschied zwischen Theorie und Praxis gilt:
Aber selbst wenn die Dicke berücksichtigt wird (im „paraxialen Abbildungsmodell“) mit einigen
die Linsen werden als perfekt, also ohne jede optische Aberrationen angenommen.
Im falle von dünnen Linsen : alle Linsen werden als unendlich dünn angenommen.
Es wird monochromes Licht verwendet.
The model assumes sin(x) = x, which is an approximation that holds only very close to the optical axis.
gearbeitet.
Es gibt gute und schlechte Neuigkeiten:
Wir notieren ausserdem :
Objekte in verschiedenenn Entfernungen resultieren i CoCs unterschiedlicher Größe.
Die „akzeptierbare“ Maximalgröße des Coc CoC resultiert in der sogenannten „Schärfentiefe“:
Die theoretische Größe der kleinstmöglichen CoC für eine perfekte ( sogenannte beugungsbegrenze Linsen)wird durch das sogenannte Rayleigh Kriterium beschrieben
Daumenregel:
Für weisses Lincht ist es nicht möglich CoCs kleiner als die Blendenzahl, gerechnet in Mikrometer zu erhalten. Die theoretische beste Auflösung ist die Hälfte dieser Zahl
Die theoretisch beste Auflösung ist 4um / 2 = 2um
Siehe auch Why can color cameras use lower resolution lenses than monochrome cameras?.Kann das Bild auf einem Sensor mit n Megapixeln erscheinen, dann wird die Linse oft als n Megapixel Linse bezeichnet.
Dies gilt, weil die Fläche eines 1/2″ Sensors nur 1/4 (!) der Fläche eines 1″ Sensors beträgt!. Man verliert also Faktor 4 an Megapixeln.