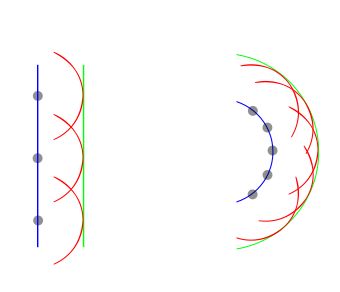
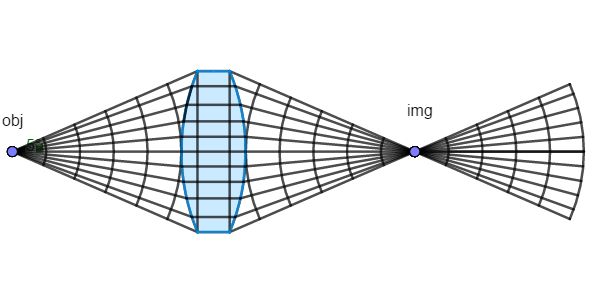
If light travels from one point to another, it takes paths of a length that in first approximation is equal to the length of optical paths length closely adjascent to the actual path.
from one point to another light always chooses a path which’s OPL does not change if the path slightly varies.
Light always takes the shortest path in terms of speed but in general not the path of shortest distance.
The actual path taken has either a maximum or a minimum OPL compared to adjascent optical paths or is equal to the OPL of adjascent paths.