Archives
Fermat’s Principle
If light travels from one point to another, it takes paths of a length that in first approximation is equal to the length of optical paths length closely adjascent to the actual path.
The actual path taken has either a maximum or a minimum OPL compared to adjascent optical paths or is equal to the OPL of adjascent paths.
Interference
Newton’s Rings
Netwon’s Rings are a phenomenon of wave optics and occur if there is a small path difference of coherent light.
They occur for example for large spheres on a glass plate with a very small gap between sphere and plate.
Some light is reflected from the glass sphere’s surface and some is reflected from the glass plate’s surface.
Because the light is coherent, we get constructive and destructive interference.
For the gap being 1/4 Lambda, the path in the gap and back is lambda/2, which results in destructive interference. Same for path lengths in the gap of 3/2 lambda, 5/2, etc. Say, for gaps that are odd multiples of lambda 1/4.
For even multiples of lambda/4, say lambda/2 , 3/2 Lambda etc, we get constructive interference.
Say, we simply can count the bright rings. For 666nm red light for example, three rings are 1000nm = 1 micrometer, which is the length of the air gap.
Newton’s rings are used in lens production, together with interferometers to find how close the current shape is from the wanted shape.
Thus surface accuracies are given in “(Newton’s) Rings”. The less rings, the better the shape got to be (and the more expensive the lens will be). Also a diametre should be given, for example five rings in 18mm diameter.
According to ISO DIN 10110 the default specs are: Wavelength 546,07 nm, 5 Rings at at 10 mm clear aperture
Below is a version of Newton Rings occuring between a sphere under test and a reference sphere
OPL
Ray
Refraction
total internal reflection
Total internal reflection (“TIR”) occurs, when the angle of incidence of a ray propagating from a higher indes medium to a lower index medium exceeds the critical angle.
![]()
[table caption=”Examples for critcal angles” width=”200″ colwidth=”100|100″ colalign=”left|left”]
![]() ,
,![]()
1.3, 50.3°
1.4, 45.6°
1.5, 41.8°
1.6, 37.8°
1.7, 36.0°
1.8,33.7°
1.9, 31.8°
2.0, 30.0°
[/table]
for an interactive example, see refraction
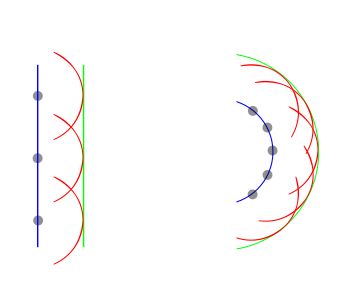
wavefront
surfaces (in mid air) of constant OPL (optical path length)
In a perfect optical system or a first order optical system all wavefronts are either planar or spherical.
Wavefronts stay after reflection perpendicular to the propagation direction of the light.