When a lens is focussed to the hyperfocal distance H, the DOF of the lens is maximized: The range of acceptable sharpness then extends from 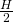 to infinity
to infinity
There are two Formulas in use:
![]()
For f=50mm, F2, and CoC = 0.03mm we get

This is the formula we use here. The results just differ in the focal length of the lens.
and
![]()
For f=50mm, F2, and CoC = 0.03mm we get
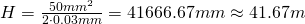
Where CoC is the circle of confusion, F is the F-number and f is the focal length of the lens.
The hyperfocal distance has curious mathematical properties:
The hyperfocal distance H is the distance at which you have to focus an object to receive the largest depth of field. If, namely, a lens is focussed to H, it is focused from ![]() to infinity.
to infinity.
When focussed to 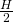 , so everything from
, so everything from 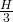 to
to 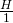 focused.
focused.
When focussed to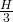 , so everything from
, so everything from 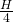 to
to 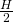 focused.
focused.
When focussed to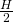 , so everything from
, so everything from 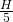 to
to 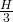 focused.
focused.
…
When focussed to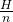 , so everything from
, so everything from 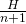 to
to 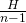 focused.
focused.
When focussed to
When focussed to
…
When focussed to
The distance
![]()
is the Depth of field.
Notice:
The depth of field is getting smaller, the larger is n, say the shorter the working distance is!