surfaces (in mid air) of constant OPL (optical path length)
In a perfect optical system or a first order optical system all wavefronts are either planar or spherical.
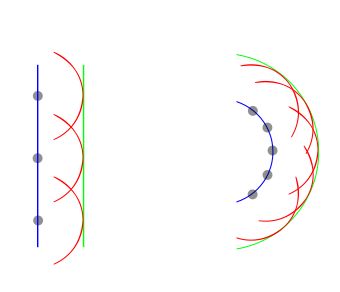
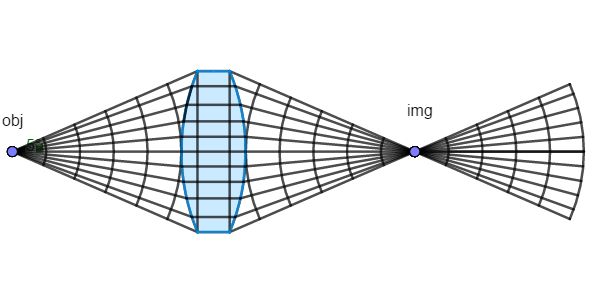
Wavefronts stay after reflection perpendicular to the propagation direction of the light.
number of wavelengths per cm
[table caption=”sample wavenumbers” width=”300″ colwidth=”100|100|100″ colalign=”left|left|left”]
wavenumber (cm^-1),wavelength (um),frequency (THz)
22727,0.440,682
18181,0.550,545
15152,0.660,455
11765,850,353
10000,1,300
1000,10,30
[/table]
Entocentric lens with a focal length smaller than the sensor diagonal, eg an f = 6mm lens on a 1/2″ sensor (the sensor size has 8mm).
When we use the word “wide angle lens”, it must be clear what sensor is used.
The same lens can, depending on the sensor, be wide-angle, telephoto lens and normal lens.
A
lens of f = 8mm on a 1/3 “sensor (6mm diagonal) a slight telephoto
lens.
On a 1/2 “Sensor (8mm diagonal) it is a
normal lens and on a 2/3” sensor (with 11mm diagonal) a wide-angle
lens.
see discussion under normal lens
Distance between mechanical front of lens and object.
When you insert distance rings between camera and
lens you might have noticed that the image gets darker and the
field of view gets smaller.
As the
lens was not changed, the
F-number of the
lens still must be the same. The darker image and the reduced
field of view are described by the working
F-number, also called effective
F-number.
The F-number 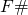 is only defined for objects at infinite distance.
is only defined for objects at infinite distance.
The sensor has according the definition of the focal length exactly the distance “focal loength” from the principal plane when the lens is focussed to infinity.
When an object comes closer, it’s image moves in the same direction. It moves further away from the principal plane.
To keep the object focussed, the distance of lens and sensor must be increased. This is equivalent with adding distance rings reagrding the infinity position of the lens. As result the images gets darker the field of view gets smaller , the therefore the magnification 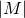 changes.
changes.
It holds:
where
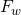 working F-number or effective F-number.
working F-number or effective F-number.
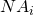 image side numerical apertur,
image side numerical apertur,
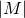 the magnification for this focus distance and
the magnification for this focus distance and
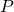 is the pupil magnification.
is the pupil magnification.
Especially:
For an objective used for a 1:1 mapping holds:
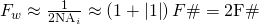
The effective F-number can also be described by the height “delta” of the inserted distance rings:
because
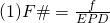 and
and
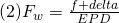
From (1) we get
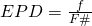
with this we get from (2) :
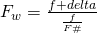
From this we can derive a third way to calculate the working F# :
From above we learnt
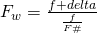
With the length of the needed distance rings delta
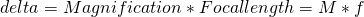
we get
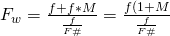
or shorter
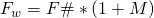
q.e.d.
see also:
F-Number
Pupil magnification
Numerical Aperture

