Archives

2 A B C D E F G H I K L M N O P R S T U V W
Na Nc Ne No Nu Ny

near point

closest point on optical axis with an image that has „acceptable sharpness“

NearPoint = \frac{(FocalLength^2 \cdot ObjectDistance)}{(FocalLength^2 + F\# \cdot CoC \cdot (ObjectDistance - FocalLength))}

Where CoC is the Circle of Confusion (the largest accepted Airy-disk) in Millimeter.

Alternatively, we can express the NearPoint using the magnification M :

NearPoint = \frac{(FocalLength^2 \cdot (M + 1))}{(FocalLength \cdot M + F\# \cdot CoC )}

If we use for example a 1/2.5″ 5 Aptina Megapixel greyscale Sensor mit 2.2\mu pixel pitch, we can use the pixel diagonal as CoC for crisp images, say CoC = 2.2\mu \cdot \sqrt{2} = 3.1 \mu = 0.0031mm
A 5 Mega lens with f=7.2mm focal length and F-stop F2.4, focused to an object distance of 100mm then has a far point of
FarPoint = \frac{((7.2mm)^2 \cdot 100mm)}{((7.2mm)^2 - 2.4 \cdot 0.0031mm \cdot (100mm-7.2mm))} = 101.35mm
und einen Nahpunkt von
NearPoint = \frac{((7.2mm)^2 \cdot 100mm)}{((7.2mm)^2 + 2.4 \cdot 0.0031mm \cdot (100mm-7.2mm))} = 98.69mm
and thus DOF = FarPoint - NearPoint = 2.66mm
If instead we use a 5 Megapixel greyscale Sony Sensor with 3.45\mu pixel pitch, we can choose as CoC the diagonal of the pixel for crisp images, say CoC = 3.45 \cdot \sqrt{2} = 4.86 \mu = 0.00486mm
A 5 Mega lens with f=7.2mm focal length and F-stop F2.4, focussed to 100mm then results in
FarPoint = \frac{((7.2mm)^2 \cdot 100mm)}{((7.2mm)^2 - 2.4 \cdot 0.00486mm \cdot (100mm-7.2mm))} = 102.13mm
and a nearpoint of
NearPoint = \frac{((7.2mm)^2 \cdot 100mm)}{((7.2mm)^2 + 2.4 \cdot 0.00486 \cdot (100-7.2))} = 97.95
thus we get DOF = FarPoint - NearPoint = 4.18mm
If we use a color sensor instead we can use CoC=2 \cdot PixelSize for crisp images. For the two sensors above we then get:
DOF_{5 Mega Aptina} = 101.93mm - 98.14mm = 3.78mm
DOF_{5 Mega Sony} = 103.06mm - 97.11mm = 5.93mm
To increase the DOF we can increase the Pixel Size, but we either lose resolution, or (at the same pixel count) the magnification changes)
If you change the focal length of a lens in a way, that (with the same sensor) you get the same FOV (then from a different distance) this results in the same DOF !!!
see also https://www.optowiki.info/blog/can-i-increase-the-dof-by-changing-the-focal-length/
To increase the DOF we can keep the working distance and the pixel size while reducing the sensor size, but then we lose resolution (because less of the same size pixels fit on the now smaller sensor)
When a lens is focussed to the hyperfocal distance H, the far point is at \infty and the near point is at \frac{H}{2}.
The DOF is \infty then, thus focussing to the hyperfocal distance results in the largest possible DOF.

Yet another way to express the Near-Point is to use the Hyperfocal distance H :
H = \frac{f^2}{F \cdot CoC} + f

If the lens is then focused to some object distance OD, this OD can be expressed as fraction of H :

OD = \frac{H}{x}

or

x = \frac{H}{OD}

Then the near point is
NearPoint = \frac{H}{x+1},

the far point is
FarPoint = \frac{H}{x-1}

and the Depth of field is
DOF = FarPoint - NearPoint = \frac{H}{x-1} - \frac{H}{x+1}

When we set the object distance OD to the hyperfocal distance H, we get:
OD = H
Therefore from
x = \frac{H}{OD}
we get
x = 1.
This means however, that
FarPoint = \frac{H}{x-1} = \infty
and therefore,
DOF = FarPoint - NearPoint = \infty - H/2 = \infty
For a lens with f=12mm, F#=2.8 and a CoC of 3.1um we get
H = \frac{12^2}{2.8 \cdot 0.0031} + 12 = 16602mm

For OD = 200mm we get
x = \frac{H}{OD} = \frac{16602}{200} = 83.01mm
So, with
FarPoint = \frac{H}{x-1} = \frac{16602mm}{83.01mm-1mm} = 202.44
and
NearPoint = \frac{H}{x+1} - \frac{16602mm}{83.01mm+1mm} = 197.62
we get
DOF = FarPoint - NearPoint = 202.44 - 197.62 = 4.82mm

For OD = 100mm we get
x = \frac{H}{OD} = \frac{16602}{100} = 166mm
So, with
FarPoint = \frac{H}{x-1} = \frac{16602mm}{166mm-1mm} = 100.62
and
NearPoint = \frac{H}{x+1} - \frac{16602mm}{166mm+1mm} = 99.41
we get
DOF = FarPoint - NearPoint = 100.62 - 99.41 = 1.21mm

Therefore by decreasing the OD by factor 2, the DOF decreased by factor 4.

When the magnification increases by factor 2, the DOF decreases by factor 4

or, equivalent :

When the object distance decreases by factor 2, the DOF decreases by factor 4

Newton’s Rings

Netwon’s Rings are a phenomenon of wave optics and occur if there is a small path difference of coherent light.
They occur for example for large spheres on a glass plate with a very small gap between sphere and plate.

Some light is reflected from the glass sphere’s surface and some is reflected from the glass plate’s surface.
Because the light is coherent, we get constructive and destructive interference.

For the gap being 1/4 Lambda, the path in the gap and back is lambda/2, which results in destructive interference. Same for path lengths in the gap of 3/2 lambda, 5/2, etc. Say, for gaps that are odd multiples of lambda 1/4.
For even multiples of lambda/4, say lambda/2 , 3/2 Lambda etc, we get constructive interference.

Say, we simply can count the bright rings. For 666nm red light for example, three rings are 1000nm = 1 micrometer, which is the length of the air gap.

Newton’s rings are used in lens production, together with interferometers to find how close the current shape is from the wanted shape.

Thus surface accuracies are given in “(Newton’s) Rings”. The less rings, the better the shape got to be (and the more expensive the lens will be). Also a diametre should be given, for example five rings in 18mm diameter.

According to ISO DIN 10110 the default specs are: Wavelength 546,07 nm, 5 Rings at at 10 mm clear aperture

Below is a version of Newton Rings occuring between a sphere under test and a reference sphere

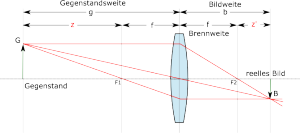
Newtonian Image Equation

newton-linsengleichung

Image formation of a lens. The values z und z’ are marked red.

The Newtonian equation is an equation of ray optics named after the English physicist Isaac Newton.

It reads
f^2 = z \cdot z'

with

z = ObjectDistance - FocalLength

and

z'= ImageDistance - FocalLength

Solved for ObjectDistance we get:

ObjectDistance = FocalLength + \frac {f^2}{ImageDistance - FocalLength}

Solved for ImageDistance we get:

ImageDistance = FocalLength + \frac {f^2}{ObjectDistance - FocalLength}

This Newtonian Image equation is often used instead of the “lens equation”. Here z is the differences between object distance and focal length and z ‘ is the difference between image distance and focal length.

Be an object point 20mm left of the first Focal point of a lens of 30mm focal length.
Then it’s image is -\frac{30 * 30}{-20} = 45mm to the right of the second Focal point (“-” 20 because the left of the focal point).
Be an object point 10mm left of the first Focal point of a lens of 30mm focal length.
Then it’s image is -\frac{30 * 30}{-10} = 90mm to the right of the second focal point (“-” 10 because the left of the focal point).

The advantage of Newton’s equation is that you can determine the focal point and distances from these focal points of lenses relatively easy, while principal points can be relatively difficult to determine.

normal lens

Entocentric lens with a focal length equal to the sensor diagonal.



For SLR cameras (film 24x36mm, 42mm diagonal) is an f = 42mm a normal lens. Previously f = 50mm lenses are called normal lens (well, f = 50mm was close to f = 42mm)
Third inch lens (6mm sensor diagonal) of f = 6mm focal length are normal lenses.
Half-inch lenses of f = 8mm are normal lenses.
One-inch lenses of f = 16mm are normal lenses.
A third inch lens with f = 6mm lens and a half-inch lens of f = 8mm
 have the same field of view!

Normal lenses help to define “wide angle lens” and “telephoto lenses”: 

Lenses with a focal length less than that of a normal lens is called wide angle lens.
Lenses with a focal length greater than that of a normal lens are called telephoto lens.

However, an f = 8mm lens on a 1/3 sensor is a “(slight”) “tele lens and on a 1” sensor, a wide angle lens.

Numerical Aperture

The Numerical Aperture (“NA”) is a measure for the resolution of a lens.

At given working distance the diffraction limited lens like a telecentric lens with the higher Numerical Aperture has the better resolution

The Numerical Aperture is calculated as sine of half the aperture angle multiplied by the refraction index of the media.

According to Snells Law, the Numerical aperture of the lens stays constant across various media :
NA = n_1 \sin(\theta_1) = n_2 \sin(\theta_2) =...

NA = n \sin(\theta) = n \sin(atan(\frac {EntrancePupilDiameter}{2 FocalLength}))

From the NA , you can calulate the F-Number of a lens from the above equition with n about 1 and because (for small angles sin(x) is about tan(x)) to a simplified:

F\# = \frac{1}{2 NA}

If magnification and pupil magnification P are known, we can calculate the effective F-number :

WorkingF\# = \frac{1}{2 NA_{image}} = (1- \frac{magnification}{P}) F\#

and also

\frac{1}{2 NA_{object}} = (\frac{magnification - P}{magnification P}) F\#

With the object distance increasing to infinity, the Working F# nears the F#.