lens equation | OptoWiki Knowledge Base

The “Gauss lens equation,” as it is known, goes like this:

$\frac{1}{f} = \frac{1}{g} + \frac{1}{b}$

where
f = focal length,
g = distance to object (measured from object side principal plane H).
b = distance to image (measured from image side principal plane H’).

It can be solved for focal length, object distance and image distance.

We may find the focal length by this equation:

$f = \frac {1} {\frac {1} {g} + \frac {1} {b}}= \frac {1}{\frac {g + b}{g \cdot b}}=\frac {g \cdot b}{g + b}$

We may find the object distance by this equation:

$g = \frac {1} {\frac {1} {f} - \frac {1} {b}}=\frac{f \cdot b}{b - f}$

We may find the image distance by this equation:

$b = \frac {1} {\frac {1} {f} - \frac {1} {g}} = \frac {f \cdot g}{g - f}$

Interpretation of the lens equation

What can be derived from this formula?

The focus plane contains the image of infinitely far away objects.

When the object moves to infinity (= when g gets infinitely large), then

$\frac {1} {g} \rightarrow 0$
And therefore $b = f$

On the object side, an object with a double focal length distance is mapped to an image with a double focus length distance on the image side.

In other words : If we want a 1:1 mapping in distance X from the sensor you have to choose

$f = \frac {X}{4}$

(but subtract the distance of the principal points from X)

The picture is at infinity when the object distance equals the focus length.

When an object nears to the focus length, the image distance rises. Therefore $\frac {1} {b} \rightarrow 0 holds$ .

For an object closer to the lens than the focal length $\frac {1} {DistanceToImage} < 0$ holds: the image is generated on the object side (!) of the lens.

The object and image distances are calculated from the primary planes on the object and image sides, respectively.
As a result, the object distance differs from the working distance in most cases.

The focal length is a paraxial concept. Therefore the Gauss lens equation is only valid in the paraxial region of the lens, the region where 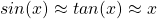$sin(x) \approx tan(x) \approx x$ holds. Most calculators don’t care (including ours), As a result, anytime larger viewing angles are involved, the results are essentially a “informed guess.”