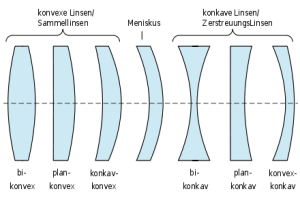
A lens element is a component made of an optical transparent material (usually glass) with two optical active surfaces.
“optical transparent” does not necessarily mean that the component is transparent for human eyes!
For example are lenses made of Germanium not transparent for humans. For certain cameras they are transparent however.
Lenses can be used to focus
light
![Lens_and_wavefronts[1]](https://www.optowiki.info/wp-content/uploads/2013/06/Lens_and_wavefronts1.gif)
The main effect of lenses is that they map object points to image points.
Let say we have two object points, for example the Top T0 and the bottom B0 of a vase. A two element compound lens works like this :
The object points T0 an B0 are mapped to image points T1 and B1 by lens element number 1. The lens elements are numbered starting from object side.
The images T1 and B1 then become the new “object points” of lens element 2 and map T1 and B1 to “images of image” of T0 and T0, called T2 and B2″.
A lens with 10 lens elements accordingly generates sequences
T0->T1->T2->… -> T10
and
B0->B1->B2->….-> B10
The image produced by a lens can be in front or behind the lens.
It can be smaller or bigger than the object.
Of course we want images of trees to be smaller than trees.
Image of microscopic details we of course want to be larger than the details.
The “Gauss lens equation,” as it is known, goes like this:
where
f = focal length,
g = distance to object (measured from object side principal plane H).
b = distance to image (measured from image side principal plane H’).
It can be solved for focal length, object distance and image distance.
We may find the focal length by this equation:
We may find the object distance by this equation:
We may find the image distance by this equation:
Interpretation of the lens equation
What can be derived from this formula?
The object and image distances are calculated from the primary planes on the object and image sides, respectively.
As a result, the
object distance differs from the
working distance in most cases.
The
focal length is a paraxial concept. Therefore the
Gauss lens equation is only valid in the paraxial region of the
lens, the region where
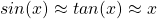
holds. Most calculators don’t care (including ours), As a result, anytime larger viewing angles are involved, the results are essentially a “informed guess.”
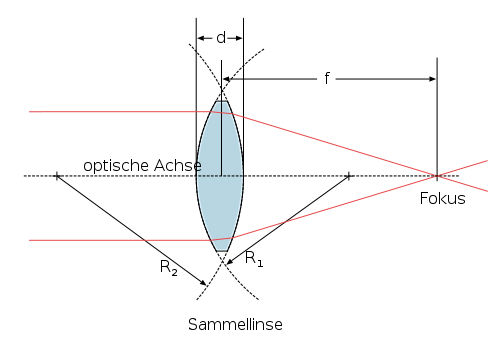
The formula (at the bottom of this post) shows for thin, spherical lenses the relationship between shape and power.
Be d center thickness of the lens element.
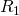 and
and  be the radii of the spheres that describe the surfaces.
be the radii of the spheres that describe the surfaces.
Keep the sign conventions for radii in mind, however!
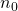 be the index of refraction of the medium outside the lens and
be the index of refraction of the medium outside the lens and
n be the index of refraction of the lens material.
f be the focallength of the lens and
D be it’s Power, 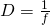
For spherical optical systems holds
generally in the paraxial region:
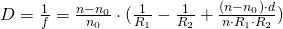
Is the surrounding medium air, we get (because
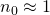
) the approximation:
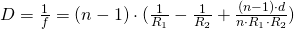
Are the lenses also
thin (idealizing
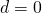
), the formula simplifies to
Lensmaker’s formula:
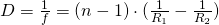
![Lens_and_wavefronts[1]](https://www.optowiki.info/wp-content/uploads/2013/06/Lens_and_wavefronts1.gif)