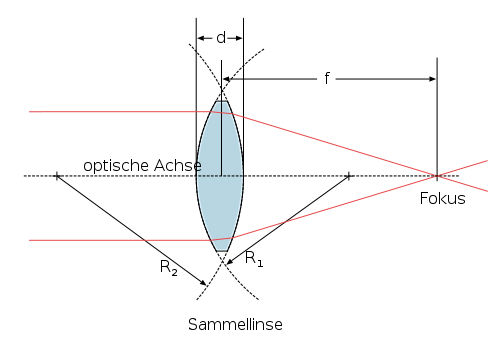
The formula (at the bottom of this post) shows for thin, spherical lenses the relationship between shape and power.
Be d center thickness of the lens element.
![]() and
and ![]() be the radii of the spheres that describe the surfaces.
be the radii of the spheres that describe the surfaces.
Keep the sign conventions for radii in mind, however!
![]() be the index of refraction of the medium outside the lens and
be the index of refraction of the medium outside the lens and
n be the index of refraction of the lens material.
f be the focallength of the lens and
D be it’s Power, ![]()
For spherical optical systems holds generally in the paraxial region:
![]()
Is the surrounding medium air, we get (because 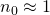 ) the approximation:
) the approximation:
![]()
Are the lenses also thin (idealizing 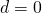 ), the formula simplifies to
), the formula simplifies to
Lensmaker’s formula:
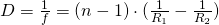
Lensmaker’s formula: