closest point on optical axis with an image that has „acceptable sharpness“
![]()
Where CoC is the Circle of Confusion (the largest accepted Airy-disk) in Millimeter.
Alternatively, we can express the NearPoint using the magnification M :
![]()
If we use for example a 1/2.5″ 5 Aptina Megapixel greyscale Sensor mit 2.2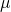 pixel pitch, we can use the pixel diagonal as CoC for crisp images, say
pixel pitch, we can use the pixel diagonal as CoC for crisp images, say 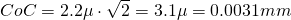
A 5 Mega lens with f=7.2mm focal length and F-stop F2.4, focused to an object distance of 100mm then has a far point of
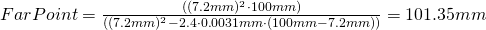
und einen Nahpunkt von
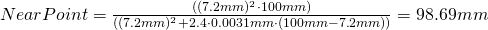
and thus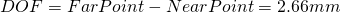
A 5 Mega lens with f=7.2mm focal length and F-stop F2.4, focused to an object distance of 100mm then has a far point of
und einen Nahpunkt von
and thus
If instead we use a 5 Megapixel greyscale Sony Sensor with 3.45 pixel pitch, we can choose as CoC the diagonal of the pixel for crisp images, say
pixel pitch, we can choose as CoC the diagonal of the pixel for crisp images, say 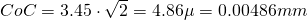
A 5 Mega lens with f=7.2mm focal length and F-stop F2.4, focussed to 100mm then results in
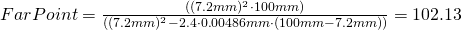 mm
mm
and a nearpoint of
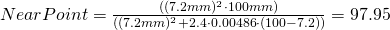
thus we get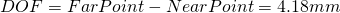
A 5 Mega lens with f=7.2mm focal length and F-stop F2.4, focussed to 100mm then results in
and a nearpoint of
thus we get
If we use a color sensor instead we can use 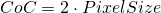 for crisp images. For the two sensors above we then get:
for crisp images. For the two sensors above we then get:
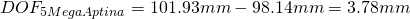
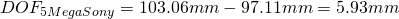
To increase the DOF we can increase the Pixel Size, but we either lose resolution, or (at the same pixel count) the magnification changes)
If you change the focal length of a lens in a way, that (with the same sensor) you get the same FOV (then from a different distance) this results in the same DOF !!!
see also https://www.optowiki.info/blog/can-i-increase-the-dof-by-changing-the-focal-length/
see also https://www.optowiki.info/blog/can-i-increase-the-dof-by-changing-the-focal-length/
To increase the DOF we can keep the working distance and the pixel size while reducing the sensor size, but then we lose resolution (because less of the same size pixels fit on the now smaller sensor)
When a lens is focussed to the hyperfocal distance H, the far point is at 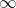 and the near point is at
and the near point is at 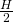 .
.
The DOF is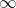 then, thus focussing to the hyperfocal distance results in the largest possible DOF.
then, thus focussing to the hyperfocal distance results in the largest possible DOF.
The DOF is
Yet another way to express the Near-Point is to use the Hyperfocal distance H :
![]()
If the lens is then focused to some object distance OD, this OD can be expressed as fraction of H :
![]()
or
![]()
Then the near point is
![]() ,
,
the far point is
![]()
and the Depth of field is
![]()
When we set the object distance OD to the hyperfocal distance H, we get:
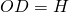
Therefore from
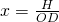
we get
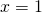 .
.
This means however, that
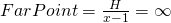
and therefore,
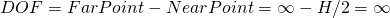
Therefore from
we get
This means however, that
and therefore,
For a lens with f=12mm, F#=2.8 and a CoC of 3.1um we get
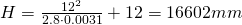
For ![]() we get
we get
![]()
So, with
![]()
and
![]()
we get
![]()
For ![]() we get
we get
![]()
So, with
![]()
and
![]()
we get
![]()
Therefore by decreasing the OD by factor 2, the DOF decreased by factor 4.
When the magnification increases by factor 2, the DOF decreases by factor 4
or, equivalent :
When the object distance decreases by factor 2, the DOF decreases by factor 4