Archives
optical axis
Optical Density
Optical density is a measure used for filters to describe how much light of a blocked wavelength still passes the filter
Abbreviation: ODn
the optical density is given by the formula:
ODn = 10^-n = 1/10^n
ODn = 10^-n = 1/10^n
OD0 = 10^-0 = 1/10^0 = 1 = 100% light passes
OD1 = 10^-1 = 1/10^1 = 0.1 = 10% light passes
OD2 = 10^-2 = 1/10^2 = 0.01 = 1% light passes
OD3 = 10^-3 = 1/10^3 = 0.001 = 0.1% light passes
OD4 = 10^-4 = 1/10^4 = 0.0001 = 0.01% light passes
OD1 = 10^-1 = 1/10^1 = 0.1 = 10% light passes
OD2 = 10^-2 = 1/10^2 = 0.01 = 1% light passes
OD3 = 10^-3 = 1/10^3 = 0.001 = 0.1% light passes
OD4 = 10^-4 = 1/10^4 = 0.0001 = 0.01% light passes
The optical density is an input value, demanded by the Application.
OD2 equals 1 percent.
For a camera of 256 intensity levels this equals 2.6 intesity values. This is not much stronger than the sensor noise.
For a camera of 256 intensity levels this equals 2.6 intesity values. This is not much stronger than the sensor noise.
OD3 entspricht 0.1 Prozent.
For a camera of 256 intensity levels this equals 0.26 intesity values. This is less than the sensor noise.
The higher the number the better the blocking.
The higher the number the more expensive the filter.
The higher the number the more expensive the filter.
Typical values for comemrcial filters are OD2,
higher quality filters have OD3
Filters ilters for outdoor use might need OD4 or higher to block too intensive sunlight.
higher quality filters have OD3
Filters ilters for outdoor use might need OD4 or higher to block too intensive sunlight.
For a + b = c we get ODa + ODb = ODc
so you can generater an OD6 filter by two OD3 filters. However, the optics should be prepared for the thicker glass then.
so you can generater an OD6 filter by two OD3 filters. However, the optics should be prepared for the thicker glass then.
optical magnification
May the width of an object be 1.6mm and the sensor width = 4.8mm
Then
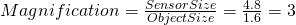
Then
May the width of an object be 36mm and the sensor width = 3.6mm
Then
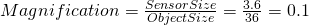
Then
Optical Path Length
The optical path length is proportional to the time light needs to travel between two points
![]()
In a homogenous medium with refractuion index n and physical point distance d this formula simplifies to
![]()
In glass with the index of refraction of 1.5 for some wavelength for a physical point distance of d=10mm the optical path length
![]()
As glass has a different index of refraction for different wavelengths, the OPL is different for each wavelength
Some OPLs for glass type BK7 and a physical point distance of d=10mm
[table caption=”sample OPLs for BK7″ width=”400″ colwidth=”100|100|100|100″ colalign=”left|left|left”]
wavelength,index of refraction,phys. distance, OPL
400nm,1.5308,10mm,15.308mm,
500nm,1.5214,10mm,15.214mm,
600nm,1.5163,10mm,15.163mm,
850nm,1.5098,10mm,15.098mm,
940nm,1.5084,10mm,15.084mm
[/table]
[table caption=”sample OPLs for BK7″ width=”400″ colwidth=”100|100|100|100″ colalign=”left|left|left”]
wavelength,index of refraction,phys. distance, OPL
400nm,1.5308,10mm,15.308mm,
500nm,1.5214,10mm,15.214mm,
600nm,1.5163,10mm,15.163mm,
850nm,1.5098,10mm,15.098mm,
940nm,1.5084,10mm,15.084mm
[/table]
In paraxial imaging system all of the light rays connecting a source point a to it’s image point have equal OLPs