Archives

2 A B C D E F G H I K L M N O P R S T U V W
Pa Pe Pi Pr Pu Px
Per Pet

pericentric

= hypercentric

With pericentric lenses objects at larger distances appear larger(!) and objects at closer distances appear smaller.

Perizentric lenses allow for example to view a can from top and the sides at the same time.

This reverses our normal viewing experience.

Pericentric lenses got to be MUCH larger than the object under inspection.

see “comparison: entocentric – telecentric – pericentric”

Application : A cylinder with a drilling that is centered on one circular side and decentered on the opposite side is to be inspected for foreign parts in the drilling.
The rotation of the cylinder is not known, so we would need a lens that can look from all sides “outside-in” at the correct angle.
Solution: DIY with the help of a Fresnel Lens, a normal M12 lens and the graphic calculator below …

Petzval Sum

In optical lens design the Petzval sum describes the image curvature of an optical system.

The formula was developed by Josef Maximilian Petzval and published 1843.

For a series of thin lenses holds

    \[\frac{1}{r_p} = \sum \limits_{i} \frac{1}{n_i \cdot f_i}\]

or more general

    \[\frac {1}{r_{p}}=n_{k+1}\sum \limits_{i=1}^{k}{\begin{cases}{\frac {1}{r_{i}}}\left({\frac {1}{n_{i}}}-{\frac {1}{n_{i+1}}}\right),&{\text{refractive surface}}\\{\frac {2}{r_{i}}},&{\text{reflective surface}}\end{cases}}\]

where:
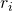r_{i} : radius of the i’th surface,
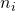n_{i} : refraction index before the refraction
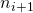n_{i+1} : refraction index after the refraction

The displacement of an image point at height 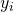y_i from the paraxial image plane is

    \[ \Delta{x} = \frac{y_{i}^2}{2} \sum \limits_{i=1}^{k}\frac{1}{n_{i} \cdot f_{i}} \]

The Petzval condition says that the curvature of the Petzval area is zero if the Petzval sum is zero.

If in addition there is no astigmatism, then the image surface is flat.

If there is astigmatism however then the folowing relationship holds between the curvature of the petzval surface and the curvature of saggital and tangential surface

    \[ \frac {2}{r_{p}}= \frac {3}{r_{s}}-\frac {1}{r_{t}}\]

The mean image curvature is here the reciproke mean of tangential and saggital curvature.