Archives

2 A B C D E F G H I K L M N O P R S T U V W
Ab Ai An Ap
Abb Abc Abe

Abbe-Method

Measuring method (named after Ernst Abbe) used to determine the focal length and the position of the principal planes of a lens singlet or a lens system (=objective) on the optical axis.

How to determine the focal length:
The position of the lens is fixed and the camera (or the screen ) is moved depending on the object position, that you get a focused image (in the image center). Different object positions result in different camera- or screen distances
FocalLength = {\frac {DifferenceOfObjectpositions}{{\frac {ObjectSize}{ImageSize2}}-{\frac {ObjectSize}{ImageSize1}}}}

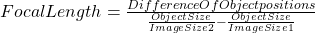
How to determine the focal length of an objective (= (= lens system)):
The Position of a lens (and the lens singlets in it) are fixed and an arbitrary Point O on the optical axis is marked as reference point, for example the center of the lens or the center of the first lens element).
Now we measure the distance x from the reference point to the object, the distance x’ to the image and the image size B.
You get a list of Magnifications
\gamma = \frac {ImageSize}{ObjectSize} = \frac{B}{G},
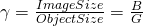and equations from refererence Point to object
x=f\left(1+{\frac {1}{\gamma }}\right)+h
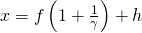
and reference point to image:
x'=f'\left(1+\gamma \right)+h'
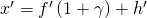
Where h und h’ are the distances from object side resp. image side principal planw to the reference point.

Abbe-number

(also known as v-number)
a measure of the materials dispersion (=variation of refractive index with wavelength),
with high values of V indicating low dispersion (low chromatic aberration).

The value Vd is given by

V_d = \frac{n_d-1}{ n_F - n_C }

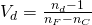
which defines the Abbe number with respect to the yellow Fraunhofer-Line d (or D3) helium line at 587.5618 nm wavelength.

It can also be defined using the green mercury E-line at 546.073 nm:

V_e = \frac{n_e-1}{ n_{F'} - n_{C'}}

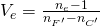
where F’ and C’ are the blue and red cadmium lines at 480.0 nm and 643.8 nm, respectively.

ABCD Matrix

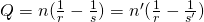
ABCD Matrixes
\begin{pmatrix} A & B \\ C & D \end{pmatrix}
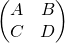
are used in paraxial optical design.

It’s only allowed to use ABCD Matrices in the paraxial range, with \sin{\theta} \approx \theta
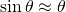
The angles are measured in radians!

A beam is described by a distance r from the optical axis and a offset angle 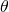\theta from the optical axis
An ABCD Matrix that describes the optical element is formed
The ABCD Matrix is multiplied by the input vector
The result is an output vector that describes the output beam with a new distance from the optical axis and a new angle off the optical axis

    \[ \left( \begin{array}{c}r'\\\theta'\end{array} \right) = \begin{pmatrix} A & B \\ C & D \end{pmatrix} \left( \begin{array}{c}r\\\theta\end{array} \right) \]

    \[ \left( \begin{array}{c}r'\\\theta'\end{array} \right) = \begin{pmatrix} A_1 & B_1 \\ C_1 & D_1 \end{pmatrix} \left( \begin{array}{c}r\\\theta\end{array} \right) \]

is a short for for the equation system

    \[r' = A_1 r + B_1 \theta \]

    \[\theta' = C_1 r + D_1 \theta \]

    \[ \left( \begin{array}{c}r''\\\theta''\end{array} \right) = \begin{pmatrix} A_2 & B_2 \\ C_2 & D_2 \end{pmatrix} \begin{pmatrix} A_1 & B_1 \\ C_1 & D_1 \end{pmatrix} \left( \begin{array}{c}r\\ \theta \end{array} \right) \]

\iff

    \[ \left( \begin{array}{c}r''\\\theta''\end{array} \right) = \begin{pmatrix} A_2 & B_2 \\ C_2 & D_2 \end{pmatrix} \left( \begin{array}{c}A_1 r + B_1 \theta\\\ C_1 r + D_1 \theta \end{array} \right) \]

\iff

    \[ \left( \begin{array}{c}r''\\\theta''\end{array} \right) = \begin{pmatrix} A_2 & B_2 \\ C_2 & D_2 \end{pmatrix} \left( \begin{array}{c}r'\\\theta'\end{array} \right) \]

with

    \[ \left( \begin{array}{c}r'\\\theta'\end{array} \right) = \begin{pmatrix} A_1 & B_1 \\ C_1 & D_1 \end{pmatrix} \left( \begin{array}{c}r\\\theta\end{array} \right) \]

\iff

    \[r'' = A_2 r' + B_2 \theta' \]

    \[\theta'' = C_2 r' + D_2 \theta' \]

with

    \[r' = A_1 r + B_1 \theta \]

    \[\theta' = C_1 r + D_1 \theta \]

\iff

    \[r'' = A_2 (A_1 r + B_1 \theta) + B_2 (C_1 r + D_1 \theta) \]

    \[\theta'' = C_2 (A_1 r + B_1 \theta) + D_2 (C_1 r + D_1 \theta) \]

\iff

    \[r'' = A_1 A_2 r + B_1 A_2 \theta + C_1 B_2 r + D_1 B_2 \theta \]

    \[\theta'' = A_1 C_2 r + B_1 C_2 \theta + C_1 D_2 r + D_1 D_2 \theta \]

\iff

    \[r'' = (A_1 A_2 + C_1 B_2 )r + (B_1 A_2 + D_1 B_2) \theta \]

    \[\theta'' = (A_1 C_2 + C_1 D_2) r + (B_1 C_2 + D_1 D_2) \theta \]

\iff

    \[ \left( \begin{array}{c}r''\\\theta''\end{array} \right) = \begin{pmatrix} A_1 A_2 + C_1 B_2 & B_1 A_2 + D_1 B_2 \\ A_1 C_2 + C_1 D_2 & B_1 C_2 + D_1 D_2 \end{pmatrix} \left( \begin{array}{c}r\\\theta\end{array} \right) \]

Examples of ABCD matrices for simple optical elements :

Propagation in free space or in a medium of constant refractive index :
\begin{pmatrix} 1 & d \\ 0 & 1 \end{pmatrix}
Where d = reduced distance= thickness / refraction index
Propagation through a series i=1..k of planparallel media with constant refraction indices 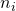n_i:

    \[ \begin{pmatrix} 1 & d_1 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & d_2 \\ 0 & 1 \end{pmatrix} ... \begin{pmatrix} 1 & d_k \\ 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & \sum\limits_{i=1}^k d_i\\ 0 & 1 \end{pmatrix} \]

Where d_i = reduced distance_i= thickness_i / refraction index_i

Refraction at a flat surface:
\begin{pmatrix} 1 & 0 \\ 0 & \frac{n_1}{n_2} \end{pmatrix}
Where:
n_1 = initial refractive index
n_2 = final refractive index
Refraction at a curved surface:
\begin{pmatrix} 1 & 0 \\ \frac{n_1 - n_2}{R n_2} & \frac{n_1}{n_2} \end{pmatrix}
Where:
R = radius of curvature, R > 0 for a convex surface (centre of curvature after interface)
n_1 = initial refractive index
n_2 = final refractive index
Reflection vrom a flat mirror:
\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}
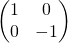
Identity matrix
Reflection from a curved mirror:
\begin{pmatrix} 1 & 0 \\ -\frac{2}{R_e} & 1 \end{pmatrix}
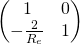
Where:
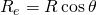
R_e = R\cos \theta effective radius of curvature in tangential plane (horizontal direction)
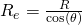
R_e = \frac{R}{\cos(\theta)} effective radius of curvature in the sagittal plane (vertical direction)
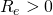
With R_e > 0 for convex mirrors (centre of curvature after interface)
Refraction at a thin lens
\begin{pmatrix} 1 & 0 \\ -\frac{1}{f} & 1 \end{pmatrix}
Where:
f = focal length of the lens, where f > 0 for convex/positive/converging lenses. Valid if if and only if the focal length is much bigger than the thickness of the lens
Refraction at a thick lens

    \[ \begin{pmatrix} 1 & 0 \\ \frac{n_2 - n_1}{R_2 n_1} & \frac{n_2}{n_1} \end{pmatrix} \begin{pmatrix} 1 & t \\ 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 \\ \frac{n_1 - n_2}{R_1 n_2} & \frac{n_1}{n_2} \end{pmatrix} \]

Where:
n_1 = refractive index outside of the lens.
n_2 = refractive index of the lens itself (inside the lens).
R_1 = Radius of curvature of First surface.
R_2 = Radius of curvature of Second surface.
t = center thickness of lens.