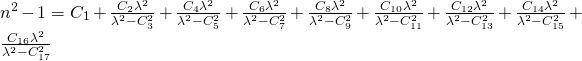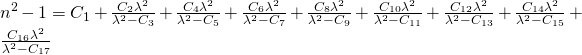Archive

A B C D E F G H K L M N O P R S T V W Z

C-Mount

Genormte Schnittstelle zur Montage von Objektiven, beschrieben in ISO 10935 (1996-12) Optik und optische Instrumente – Mikroskope – Schnittstelle Typ C

Der Durchmesser des Gewindes ist 1″ (ein Inch) und es gibt 32 Gewindegänge auf 1″ Länge.
Der Abstand zwischen dem mechanischen Anschlag des Objektivs bei Hereinschrauben und dem Sensor beträgt in Luft 17,526mm
Dies sind ziemlich genau 5mm mehr als bei CS-Mount Objektiven.
C-Mount Objektive können mit einem 5mm Verlängerungstück (C-CS-Mount Adapter) in CS-mount Kameras verwendet werden, CS-Mount Objektive aber nicht in C-Mount-Kameras.
C-Mount Objektive werden meist in der Fabrikautomation eingesetzt Objektive.

Camera Obscura

Das Prinzip der Camera Obscura (wörtlich „dunkle Kammer“ = Lochkamera) ist wie folgt:

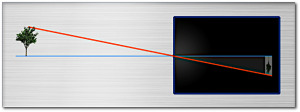
camera_obscura

Der große Nachteil ist offenbach das sehr dunkle Bild. Belichtungszeiten könenn mehrere Minuten Betragen.

Idee: WIr könnten ein gößeres Loch verwenden:

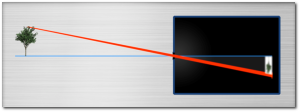
large_hole_camera_obscura

Jetzt wird das Bild jedoch nicht nur wie gewünscht heller, sondern auch verschwommen. Das Licht geht nicht nur durch die Mitte des Lochs, sondern nutzt die komplette Öffnung aus. Es wird also nicht nur der erwartete Ort des Bildes belichtet, sondern auch seine unmittelbare Umgebung.

Als Ergebnis ist das Bild eines Objektpunktes kein Punkt, sondern eine kleine Kreisscheibe (der „Unschärfekreis“, englisch: „Circle of Confusion“ = „CoC“ ).

Für weit entferne Objekte ist der Durchmesser des Zerstreuungskreises der Lochdurchmesser der Kamera!

CS-Mount

Genormte Schnittstelle zur Montage von Objektiven, beschrieben in ISO 10935 (1996-12) Optik und optische Instrumente – Mikroskope – Schnittstelle Typ CS.
Der Durchmesser des Gewindes ist 1″ (ein Inch) und es gibt 32 Gewindegänge auf 1″ Länge.
Der Abstand zwischen dem mechanischen Anschlag des Objektivs bei Hereinschrauben und dem Sensor beträgt in Luft 12,52mm.
Dies sind ziemlich genau 5mm weniger als bei C-Mount Objektiven.
Zwar können C-Mount Objektive können mit einem 5mm Verlängerungstück (C-CS-Mount Adapter) in CS-mount Kameras verwendet werden, CS-Mount Objektive aber nicht in C-Mount-Kameras.
CS-Mount Objektive werden meist in der Sicherheitstechnik verwendet, oft sind es Weitwinkel-Objektive.

Dispersion

(von lateinisch dispergere, „ausbreiten, zerstreuen“) ) :

Die Abhängigkeit einer Größe von der Frequenz, bzw. Wellenlänge.

Light_dispersion_conceptual(C) Wikipedia, zum Animieren bitte klicken

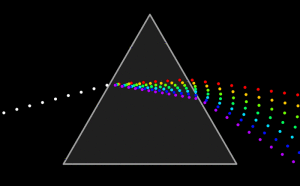
Beim Prisma führt die Dispersion zur Aufspaltung eines weissen Lichtbündels in die Einzelfarben. Ein Regenbogen, bei dem in den einzelnen Wasssertröpchen das Licht in Abhängigkeit von der Wellenlänge einen anderen Verlauf nimmt ist ein anderes Beispiel von Dispersion.

Jedes optische Medium / jeder Glastyp hat unterschiedliche Brechungsindizes für die verschiedenen  Wellenlängen. Eine Zahl die beschreibt, wie unterschiedlich die optischen Pfade der verschiedenen Wellenlängen sind, ist die Abbe-Zahl.

Unter Dispersionsformeln sind die wichtigsten Formeln aufgeführt.

Dispersionsformeln

Jedes optische Material (Gläser, Kunststoffe, Gase) hat einen anderen Brechungsindex je Wellenlänge.

Statt mit großen Tabellenwerken zu arbeiten, ist es möglich, dieses Verhalten der optischen Materialien per formel zu beschreiben.

Hier sind die gebräuchlichsten Formeln:

1: Sellmeier (bevorzugt)
n^2-1=C_1 + \frac{C_2 \lambda^2}{\lambda^2-C_3^2} + \frac{C_4 \lambda^2}{\lambda^2-C_5^2} + \frac{C_6 \lambda^2}{\lambda^2-C_7^2} + \frac{C_8 \lambda^2}{\lambda^2-C_9^2} + \frac{C_{10} \lambda^2}{\lambda^2-C_{11}^2} + \frac{C_{12} \lambda^2}{\lambda^2-C_{13}^2} + \frac{C_{14} \lambda^2}{\lambda^2-C_{15}^2} + \frac{C_{16} \lambda^2}{\lambda^2-C_{17}^2}

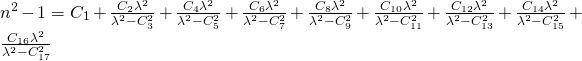
2: Sellmeier-2
n^2-1=C_1 + \frac{C_2 \lambda^2}{\lambda^2-C_3} + \frac{C_4 \lambda^2}{\lambda^2-C_5} + \frac{C_6 \lambda^2}{\lambda^2-C_7} + \frac{C_8 \lambda^2}{\lambda^2-C_9} + \frac{C_{10} \lambda^2}{\lambda^2-C_{11}} + \frac{C_{12} \lambda^2}{\lambda^2-C_{13}} + \frac{C_{14} \lambda^2}{\lambda^2-C_{15}} + \frac{C_{16} \lambda^2}{\lambda^2-C_{17}}

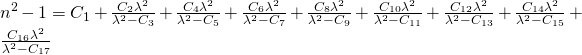
3: Polynomial
n^2 = C_1 + C_2 \lambda^{C_3} + C_4 \lambda^{C_5} + C_6 \lambda^{C_7} + C_8 \lambda^{C_9} + C_{10} \lambda^{C_{11}} + C_{12} \lambda^{C_{13}} + C_{14} \lambda^{C_{15}} + C_{16} \lambda^{C_{17}}

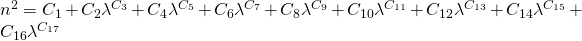
4: RefractiveIndex.info
n^2 = C_1 + \frac{C_2 \lambda^{C_3}}{\lambda^2-{C_4}^{C_5}} + \frac{C_6 \lambda^{C_7}}{\lambda^2-{C_8}^{C_9}} + C_{10} \lambda^{C_{11}} + C_{12} \lambda^{C_{13}} + C_{14} \lambda^{C_{15}} + C_{16} \lambda^{C_{17}}

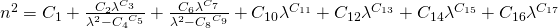
5: Cauchy
n = C_1 + C_2 \lambda^{C_3} + C_4 \lambda^{C_5} + C_6 \lambda^{C_7} + C_8 \lambda^{C_9} + C_{10} \lambda^{C_{11}}

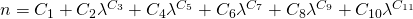
6: Gase
n-1 = C_1 + \frac{C_2}{C_3-\lambda^{-2}} + \frac{C_4}{C_5-\lambda^{-2}} + \frac{C_6}{C_7-\lambda^{-2}} + \frac{C_8}{C_9-\lambda^{-2}} + \frac{C_{10}}{C_{11}-\lambda^{-2}}

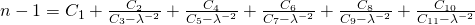
7: Herzberger
n = C_1 + \frac{C_2}{\lambda^2-0.028} + C_3 (\frac{1}{\lambda^2-0.028})^2 + C_4 \lambda^2 + C_5 \lambda^4 + C_6 \lambda^6

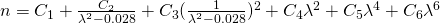
8: Retro
\frac{n^2-1}{n^2+2} = C_1 + \frac{C_2 \lambda^2}{\lambda^2-C_3} + C_4 \lambda^2

9: Exotisch
n^2 = C_1 + \frac{C_2}{\lambda^2-C_3} + \frac{C_4 (\lambda-C_5)}{(\lambda-C_5)^2 + C_6}