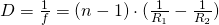Archive

A B C D E F G H K L M N O P R S T V W Z
La Lc Le Li Lo

Laser

Was ist ein Laser?

„Laser“ ist ein Akronym für „Light Amplification by Stimulated Emission of Radiation“ (Lichtverstärkung durch stimulierte Emission von Strahlung). Laserlicht ist monochrom ( hat nur eine Wellenlänge) und ist polarisiert.

Herausforderungen : Temperaturdrift kann die Frequenz eines Lasers beeinflussen, da Änderungen der Temperatur die physikalischen Eigenschaften der Laserkomponenten beeinflussen können.
Daher gibt es in (teureren) Lasern Regelkreise, die die Frequenzstabilität gewährleisten.

Laser sind also monochrom, man muss aber trotzdem z.B. beim Objektivdesign im Auge behalten, dass sich bei günstigeren Lasern die Wellenlänge des Lasers leicht mit der Temperatur ändern kann.

Die Größenordnung der Shifts kann bei 0.3-0.5 nm pro Grad Celsius betragen.

Mit steigender Temperatur nimmt die Leistung des Lasers ab.

LCoS Projektor

LCoS = Liquid Crystal on Silicon

Ein LCoS Projektor arbeitet mit polarisiertem Licht das auf Flüssigkristalle trifft und von dort reflektiert wird.
Dadurch lassen sich sehr kleine Projektoren bauen.
Der Prinzipielle Aufbau ist wie folgt :

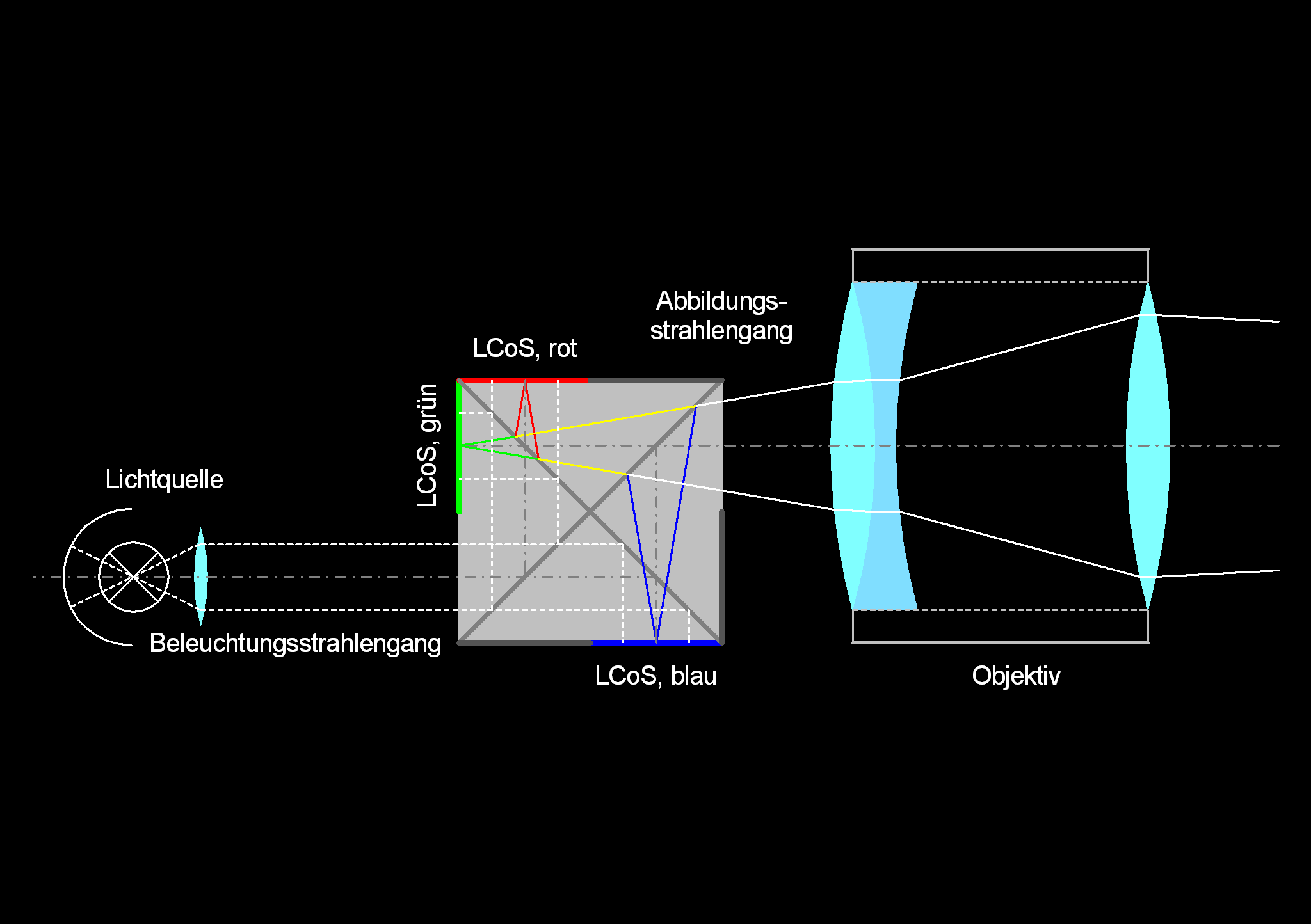
(c) Wikipedia Prinzipieller Aufbau eines LCoS Projektors

(c) Wikipedia
Prinzipieller Aufbau eines LCoS Projektors

Linse

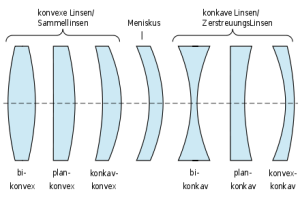
Ein Körper aus einem optischen Material (üblicherweise Glas) mit zwei optisch aktiven Flächen.

Linsen haben als wesentliche Eigenschaft, dass sie Objektpunkte in Bildpunkte abbilden.

Linse bester Form (Best Form Lens)

Linsen Bester Form (Best Form Lenses) sind speziell entwickelte Linsen, die darauf abzielen, sphärische Aberrationen zu minimieren, während sie weiterhin sphärische Oberflächen verwenden (im Gegensatz zu asphärischen Formen). Sie bieten die bestmögliche Leistung für das Kollimieren und Fokussieren von Lichtstrahlen.

Minimierung sphärischer Aberration: Best Form Lenses sind so gestaltet, dass sie die typischen Verzerrungen, die bei sphärischen Linsen auftreten können, reduzieren.
Leistungsfähigkeit: Diese Linsen sind optimal für Anwendungen, bei denen eine präzise Lichtfokussierung erforderlich ist.

For an interactive calculator see here

Linsengleichung

Die sog. Gauss’sche Linsengleichung lautet:

\frac{1}{f} = \frac{1}{g} + \frac{1}{b}

wobei
f = Brennweite
g = Gegenstandsweite ( = Entfernung vom Objekt zur objektseitigen Hauptebene) und
b = Bildweite ( = Entfernung vom Bild zur bildseitigen Hauptebene)
lautet die sog. Linsengleichung:

Auflösung nach der Brennweite

f= \frac {1} {\frac {1} {g} + \frac {1} {b}}= \frac {1}{\frac {g+ b}{g \cdot b}}=\frac {g \cdot b}{g+b}

Auflösung nach der Gegenstandsweite

g= \frac {1} {\frac {1} {f} - \frac {1} {b}}=\frac{f \cdot b}{b- f}

Auflösung nach der Bildweite

b= \frac {1} {\frac {1} {f} - \frac {1} {g}} = \frac {f \cdot g}{g- f}

Interpretation der Linsengleichung

Was kann man diesen Formeln ansehen?

  • Das Bild unendlich weit entfernter Objekte liegt in der Brennebene

Entfernt sich nämlich ein Objekt unendlich weit von der Linse (= wird die Gegenstandsweite g unendlich groß), so wird

\frac {1} {g} \rightarrow 0

Also

b= f
  • Ein Objekt das in der objektseitig doppelten Brennweite liegt, wird in Originalgrösse auf ein Bild sensorseitig in doppelter Brennweite abgebildet.
  • In anderen Worten : Möchte man eine 1:1 Abbildung in Entfernung X vom Sensor erreichen, wähle man
f = \frac {X}{4}

(von X ist noch der Abstand der Hauptebenen abzuziehen)

  • Ist die Gegenstandsweite gleich der Brennweite, so liegt das Bild im Unendlichen.
  • Je näher sich ein Objekt von Unendlich kommend der Brennweite nähert, desto ähnlicher werden Brennweite und Gegenstandsweite. Also muss :\frac {1} {b} \rightarrow 0 gehen.
  • Ein Objekt im Abstand der Brennweite vor der Linse hat sein Bild in unendlicher Entfernung (= wird auf unendlich abgebildet).
  • Für ein Objekt, das näher als als die Brennweite an eine Linse kommt, muss :\frac {1} {b} < 0 gelten. Das Bild entsteht also auf der Objektseite (!) der Linse.
Objekt- und Bildabstand werden von den objektseitigen bzw. bildseitigen Hauptebenen aus gemessen.
Daher ist in den meisten Fällen der Arbeitsabstand und der Objektabstand unterschiedlich.
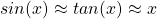
Die Brennweite ist ein paraxiales Konzept.Daher gilt die Gauss’sche Linsengleichung nur im paraxialen Bereich der Linse, des Bereichs also, in dem sin(x) \approx tan(x) \approx x gilt. Die meisten Brennweitenrechner (auch unsere) kümmern sich nicht um diese Einschränkung. Als Folge muss man die Ergebnisse, wann immer eine kleine Brennweite ? ein weiter Blickwinkel eine Rolle spielt, die Ergebnisse mit Vorsicht zu geniessen. Brennweiten werden typischerweise unterschätzt

Linsenschleiferformel

(auch Linsenmacherformel und Linsenmachergleichung genannt)

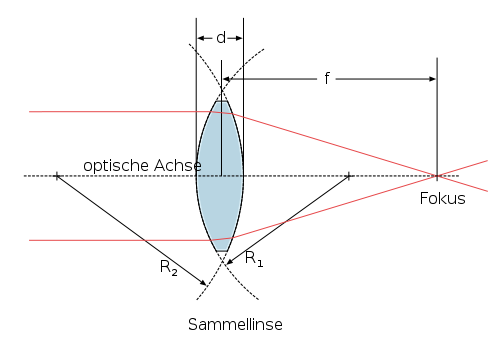
Die Formel (ganz unten auf der Seite) gibt für dünne, sphärische Linsen den Zusammenhang zwischen Form und Brechkraft an.

Es sei d die Mittendicke ( engl. center thickness) der Einzellinse.
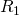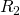R_1 und R_2 seien die Radien der Kugeln die die Oberflächen beschreiben.
Dabei sind die Vorzeichenkonventionen zu beachten!

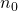n_0 sei der Brechungsindex des Mediums außerhalb der Linse und
n sei der Brechungsinsex des Linsenmaterials.

f sei die Brennweite der Linse und
D sei ihre Brechkraft, also 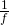\frac{1}{f}

Für sphärische optische Systeme gilt allgemein in der paraxialen Umgebung :
D = \frac{1}{f} = \frac{n-n_0}{n_0}\cdot (\frac{1}{R_1} - \frac{1}{R_2} + \frac{(n-n_0)\cdot d}{n \cdot R_1 \cdot R_2})
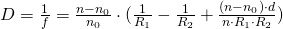
Ist das umgebende Medium Luft, so gilt näherungsweise ( wegen n_0 \approx 1 ):

D = \frac{1}{f} = (n-1)\cdot (\frac{1}{R_1} - \frac{1}{R_2} + \frac{(n-1)\cdot d}{n \cdot R_1 \cdot R_2})

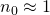
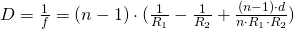
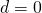
Sind die Linsen außerdem noch dünn (gilt also idealisierend d = 0), so vereinfacht sich die Formel zur
Linsenmacherformel:
D = \frac{1}{f} = (n-1)\cdot (\frac{1}{R_1} - \frac{1}{R_2})