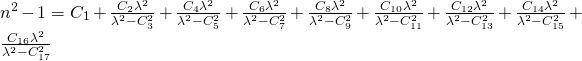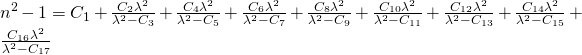Archive

A B C D E F G H K L M N O P R S T V W Z
De Di Do

Dispersion

(von lateinisch dispergere, „ausbreiten, zerstreuen“) ) :

Die Abhängigkeit einer Größe von der Frequenz, bzw. Wellenlänge.

Light_dispersion_conceptual(C) Wikipedia, zum Animieren bitte klicken

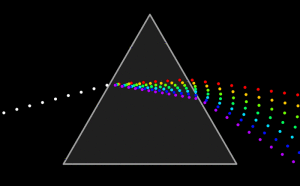
Beim Prisma führt die Dispersion zur Aufspaltung eines weissen Lichtbündels in die Einzelfarben. Ein Regenbogen, bei dem in den einzelnen Wasssertröpchen das Licht in Abhängigkeit von der Wellenlänge einen anderen Verlauf nimmt ist ein anderes Beispiel von Dispersion.

Jedes optische Medium / jeder Glastyp hat unterschiedliche Brechungsindizes für die verschiedenen  Wellenlängen. Eine Zahl die beschreibt, wie unterschiedlich die optischen Pfade der verschiedenen Wellenlängen sind, ist die Abbe-Zahl.

Unter Dispersionsformeln sind die wichtigsten Formeln aufgeführt.

Dispersionsformeln

Jedes optische Material (Gläser, Kunststoffe, Gase) hat einen anderen Brechungsindex je Wellenlänge.

Statt mit großen Tabellenwerken zu arbeiten, ist es möglich, dieses Verhalten der optischen Materialien per formel zu beschreiben.

Hier sind die gebräuchlichsten Formeln:

1: Sellmeier (bevorzugt)
n^2-1=C_1 + \frac{C_2 \lambda^2}{\lambda^2-C_3^2} + \frac{C_4 \lambda^2}{\lambda^2-C_5^2} + \frac{C_6 \lambda^2}{\lambda^2-C_7^2} + \frac{C_8 \lambda^2}{\lambda^2-C_9^2} + \frac{C_{10} \lambda^2}{\lambda^2-C_{11}^2} + \frac{C_{12} \lambda^2}{\lambda^2-C_{13}^2} + \frac{C_{14} \lambda^2}{\lambda^2-C_{15}^2} + \frac{C_{16} \lambda^2}{\lambda^2-C_{17}^2}

2: Sellmeier-2
n^2-1=C_1 + \frac{C_2 \lambda^2}{\lambda^2-C_3} + \frac{C_4 \lambda^2}{\lambda^2-C_5} + \frac{C_6 \lambda^2}{\lambda^2-C_7} + \frac{C_8 \lambda^2}{\lambda^2-C_9} + \frac{C_{10} \lambda^2}{\lambda^2-C_{11}} + \frac{C_{12} \lambda^2}{\lambda^2-C_{13}} + \frac{C_{14} \lambda^2}{\lambda^2-C_{15}} + \frac{C_{16} \lambda^2}{\lambda^2-C_{17}}

3: Polynomial
n^2 = C_1 + C_2 \lambda^{C_3} + C_4 \lambda^{C_5} + C_6 \lambda^{C_7} + C_8 \lambda^{C_9} + C_{10} \lambda^{C_{11}} + C_{12} \lambda^{C_{13}} + C_{14} \lambda^{C_{15}} + C_{16} \lambda^{C_{17}}

4: RefractiveIndex.info
n^2 = C_1 + \frac{C_2 \lambda^{C_3}}{\lambda^2-{C_4}^{C_5}} + \frac{C_6 \lambda^{C_7}}{\lambda^2-{C_8}^{C_9}} + C_{10} \lambda^{C_{11}} + C_{12} \lambda^{C_{13}} + C_{14} \lambda^{C_{15}} + C_{16} \lambda^{C_{17}}

5: Cauchy
n = C_1 + C_2 \lambda^{C_3} + C_4 \lambda^{C_5} + C_6 \lambda^{C_7} + C_8 \lambda^{C_9} + C_{10} \lambda^{C_{11}}

6: Gase
n-1 = C_1 + \frac{C_2}{C_3-\lambda^{-2}} + \frac{C_4}{C_5-\lambda^{-2}} + \frac{C_6}{C_7-\lambda^{-2}} + \frac{C_8}{C_9-\lambda^{-2}} + \frac{C_{10}}{C_{11}-\lambda^{-2}}

7: Herzberger
n = C_1 + \frac{C_2}{\lambda^2-0.028} + C_3 (\frac{1}{\lambda^2-0.028})^2 + C_4 \lambda^2 + C_5 \lambda^4 + C_6 \lambda^6

8: Retro
\frac{n^2-1}{n^2+2} = C_1 + \frac{C_2 \lambda^2}{\lambda^2-C_3} + C_4 \lambda^2

9: Exotisch
n^2 = C_1 + \frac{C_2}{\lambda^2-C_3} + \frac{C_4 (\lambda-C_5)}{(\lambda-C_5)^2 + C_6}